The BNMA BN Repository
This repository is a resource for posting and downloading Bayesian network models for sharing with others and for providing supporting material for publications. Please respect authors' rights where noted.
Search
14 BNs found.
Wet Grass
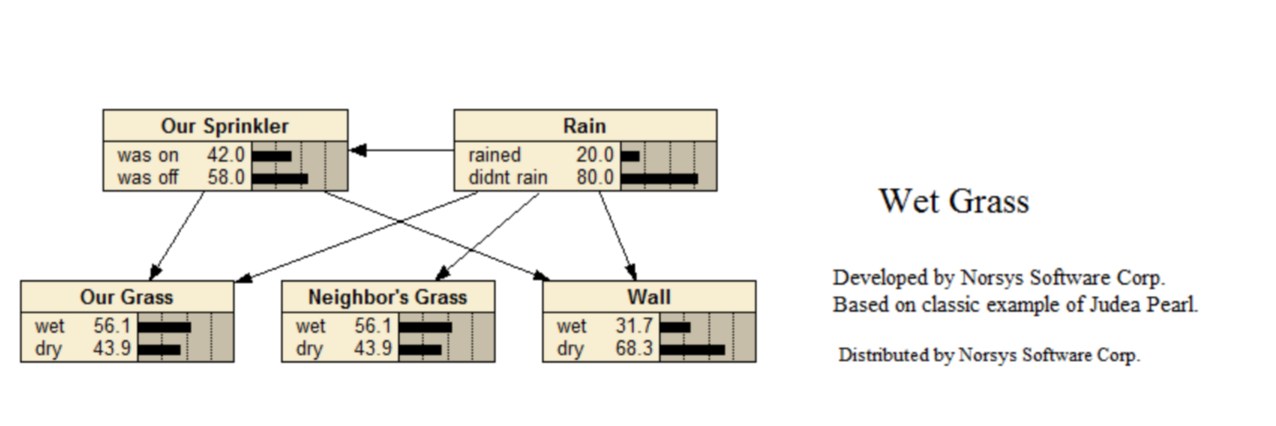
Many belief network researchers have used networks similar to this (possibly not containing nodes 'Neighbor's Grass' or 'Wall') to demonstrate "explaining away", and how rule based or evidence support systems may do incorrect chaining with these types of situations. For instance, they may combine the rules "If the ground is wet then it is likely it rained" with "If the sprinkler was on then it is likely the ground is wet" to get "If the sprinkler is on then it is likely it rained" when in fact the opposite is true. For example see Judea Pearl (1988) Probabilistic Reasoning in Intelligent Systems, p. 7. The probabilities for this network were chosen by Norsys.
Paper link: <www.norsys.com...>
Separable 2
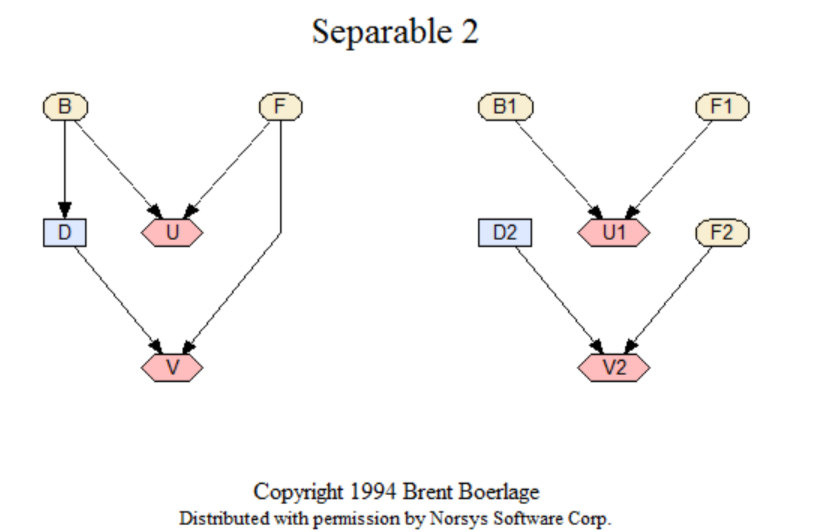
A simple example of a separable (termed 'abnormal' by Zhang) decision net, and the 2 nets it can be separated into. See Separable1 for an even simpler example. This network shows only dependencies, and does not include any numerical relationships.
BN link: <www.norsys.com...>
Separable 1
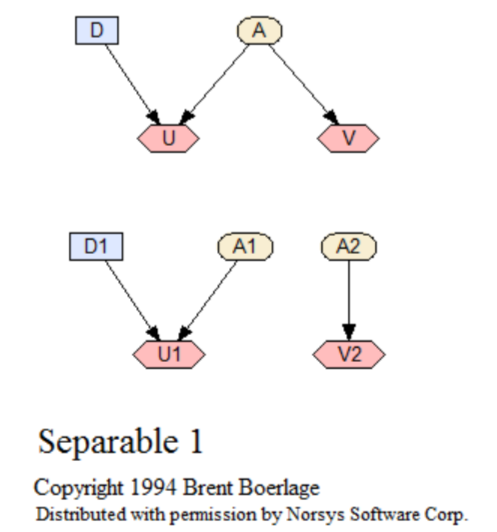
The simplest example of a separable (termed 'abnormal' by Zhang) decision net, and the 2 nets it can be separated into. This network shows only dependencies, and does not include any numerical relationships.
BN link: <www.norsys.com...>
Neapolitan90
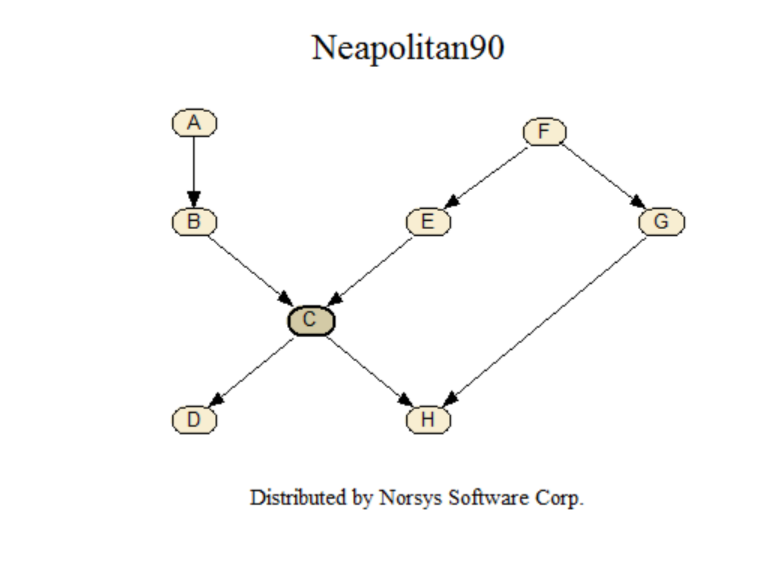
From the book Neapolitan, Richard E. (1990) Probabilistic Reasoning in Expert Systems: Theory and Algorithms, John Wiley & Sons, New York, p. 259. Started as problem 5.5.2, p.183, it becomes example 7.5, p. 261 (with diagram on p. 259), and continues numerically on p. 279. Originally based on the Lauritzen & Spiegelhalter 1988 paper.
BN link: <www.norsys.com...>
Mendel Genetics
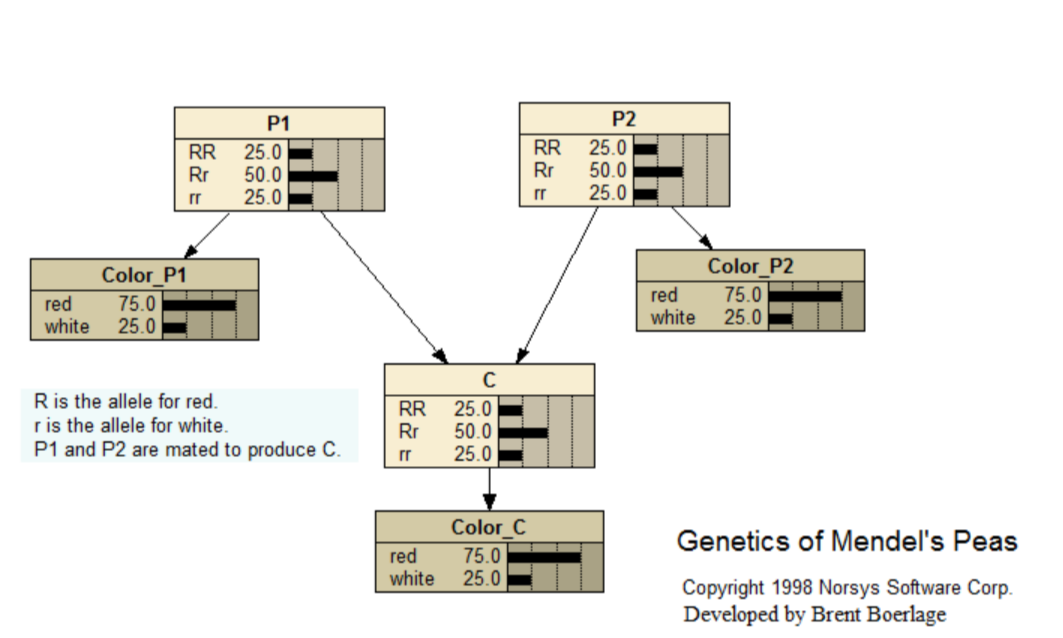
This Bayes net is for the famous experiments of Mendel, in which he developed the foundations of hereditary genetics. The experiments involved breeding red and white flowered pea plants.
A tutorial, with a complete description, is available at <www.norsys.com...>
Paper link: <www.norsys.com...>
Learn Latent
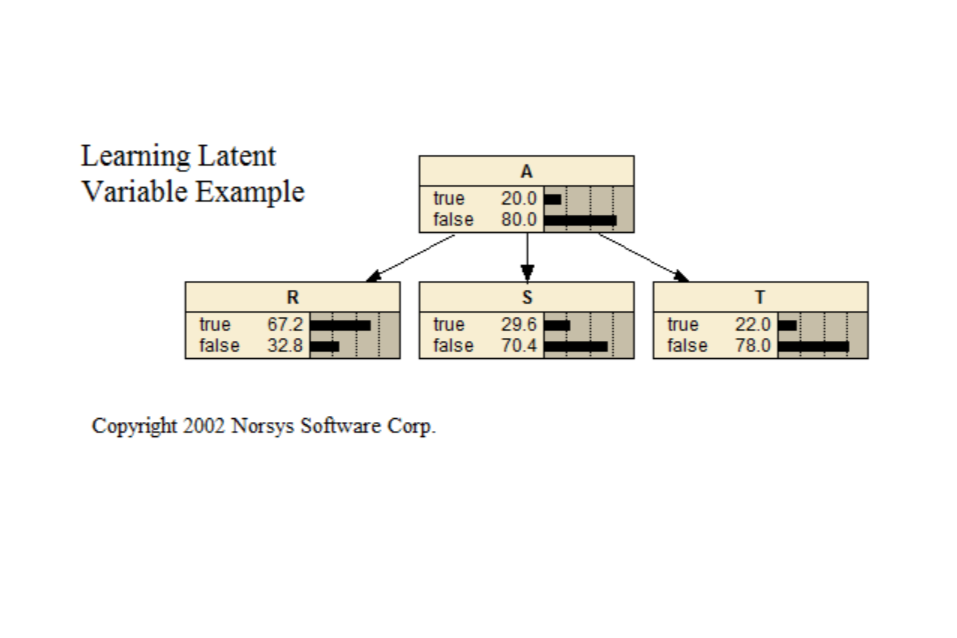
This Bayes net demonstrates learning a latent (or "hidden") variable, which occurs when you have an important node in the net for which no data appears in the case file.
Paper link: <www.norsys.com...>
Imposs Demo
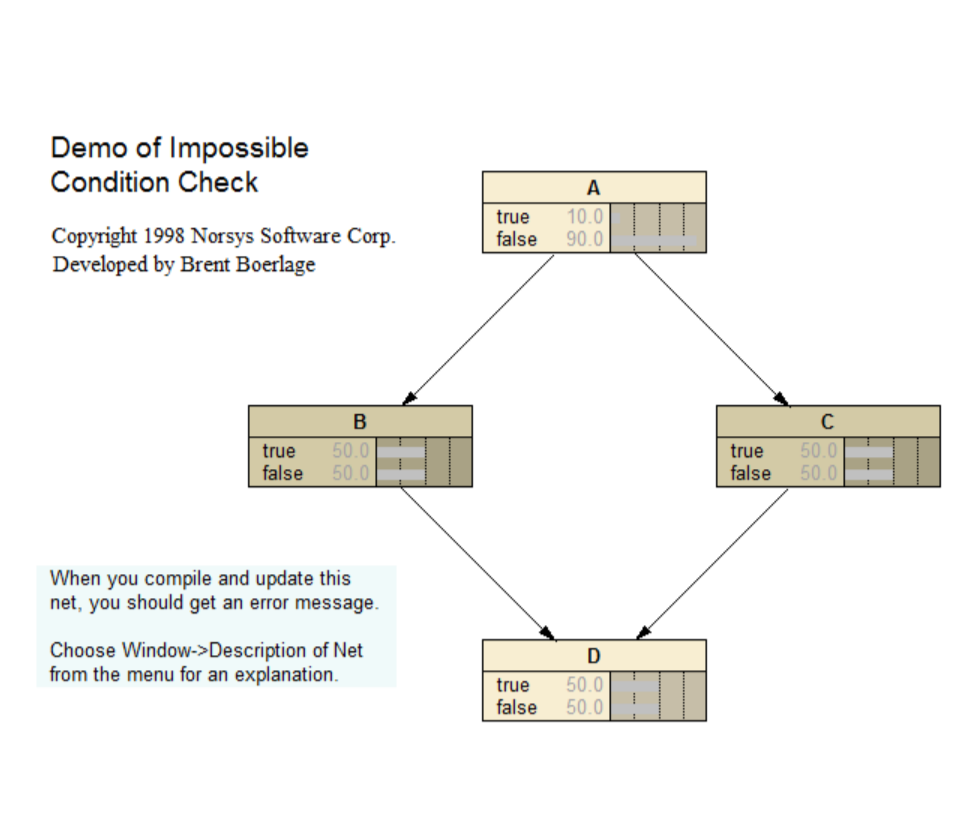
Demo of the impossible condition check. Refer to the following link for a description and tutorial of the BN: <www.norsys.com...>
Paper link: <www.norsys.com...>
False Barrier
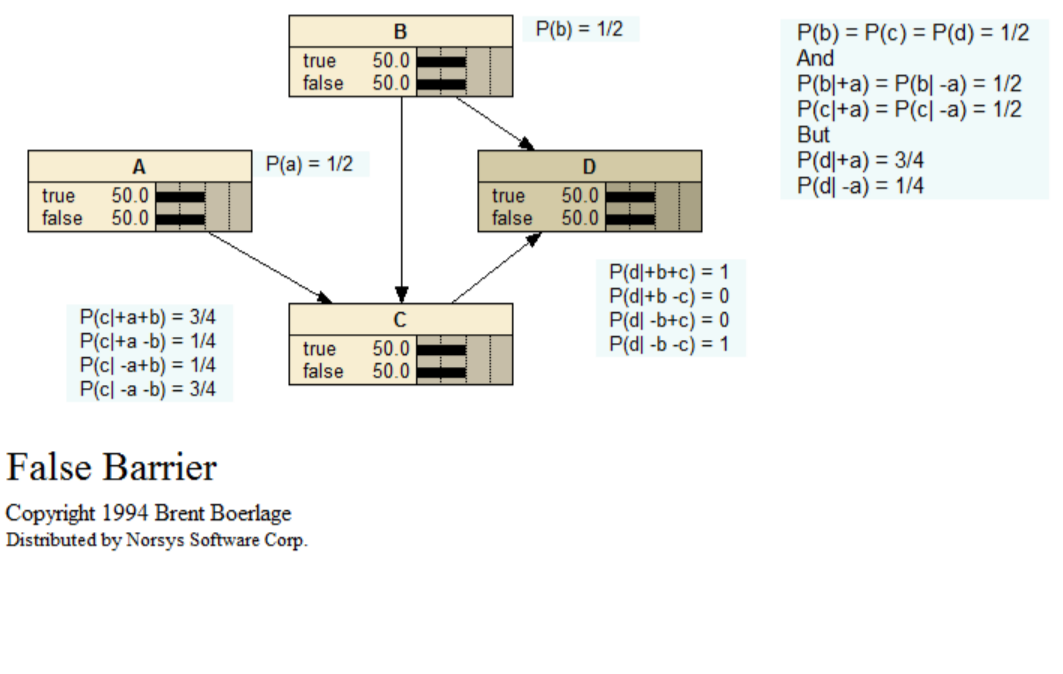
In order to express the belief in a node as a function, it must be expressed as a function of the joint beliefs of its Markov boundary nodes (i.e. the beliefs in the Cartesian product of their values). Thinking in terms of paths can obscure this. Consider the False Barrier BN illustrated:
When there is no evidence, the beliefs of A, B, C, and D are all 1/2. If we get evidence TRUE for A, the beliefs of B and C remain at 1/2, but the belief at D changes to 3/4. Thinking in terms of a constraint network, or "flow of influence along paths," it is hard to see how a change at A can create a change at D without changing the beliefs at B or C. Of course, it is the joint belief in B and C which have changed (BEL (+b+c) changes from 1/4 to 3/8, BEL(+b-c) changes from 1/4 to 1/8, etc). Therefore, we must be careful with the path concept.
Paper link: <www.norsys.com...>
Europe Map CSP
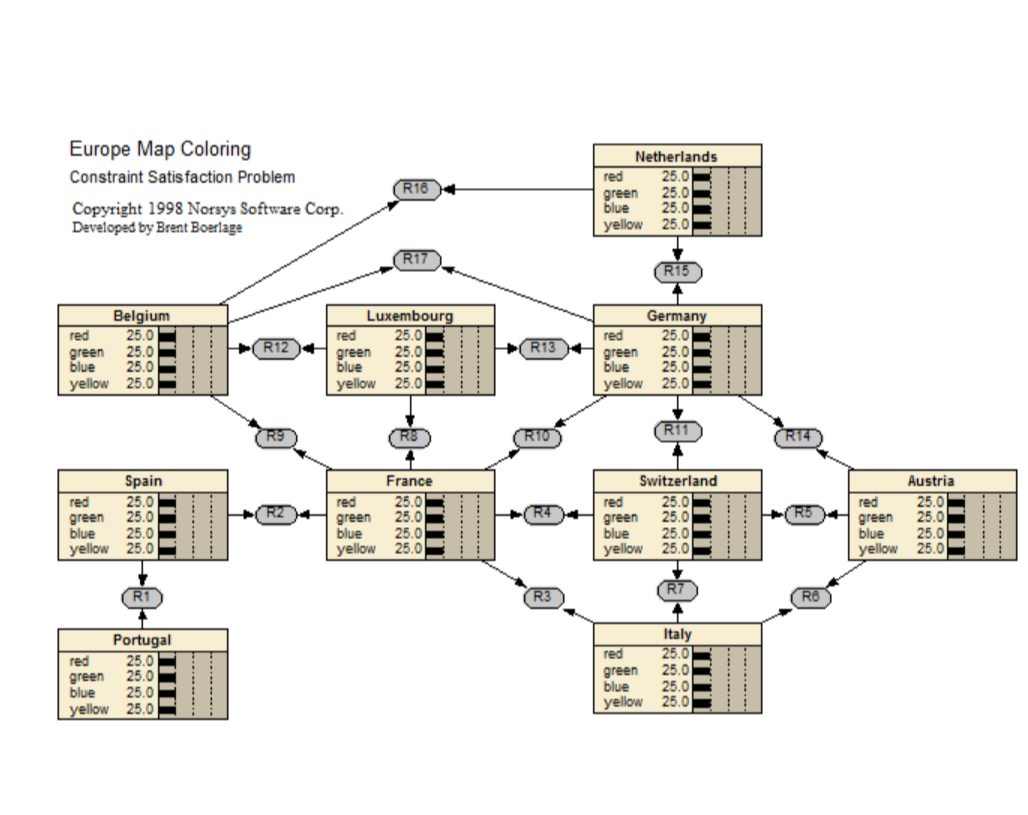
This Bayes net demonstrates how to solve constraint satisfaction problems (CSPs) using Bayes nets. A CSP consists of a number of variables, and some constraints between them. The goal is to find values for the variables that satisfy all the constraints.
Paper link: <www.norsys.com...>
Classifier Optimization
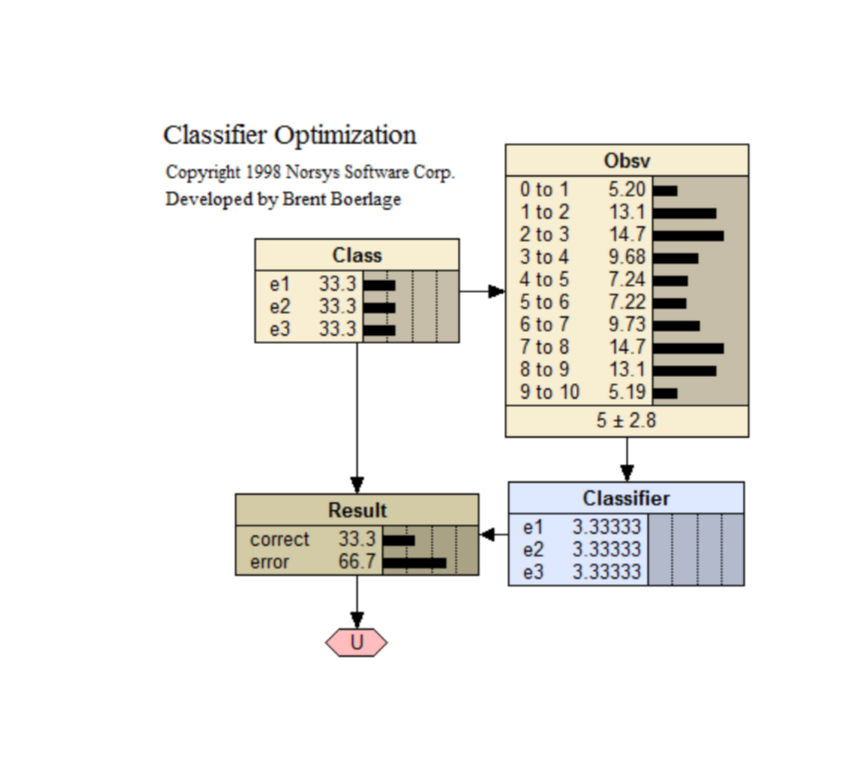
A BN classifier.
An explanation of this BN can be found at <www.norsys.com...>
Paper link: <www.norsys.com...>
Central Limit Theorem
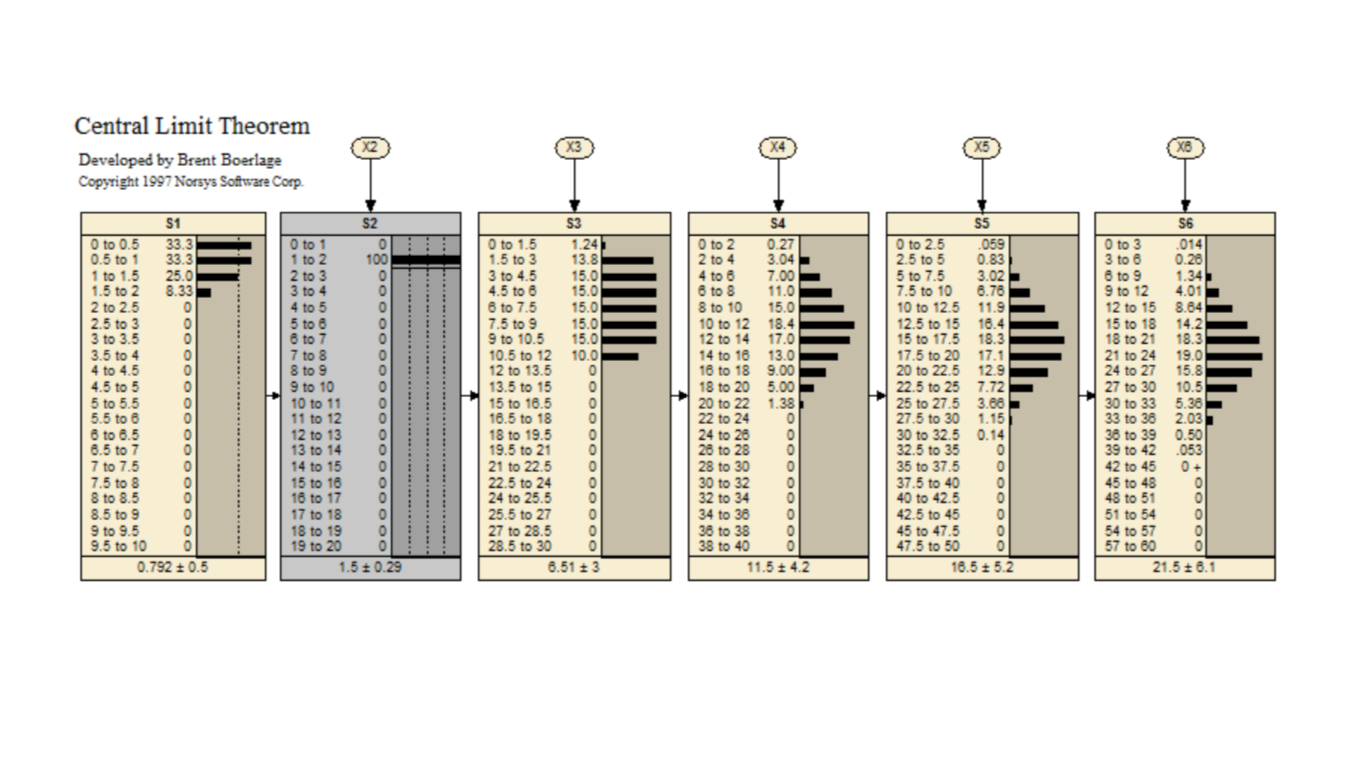
This Bayes net is to demonstrate the Central Limit Theorem.
Paper link: <www.norsys.com...>
Beta Updating
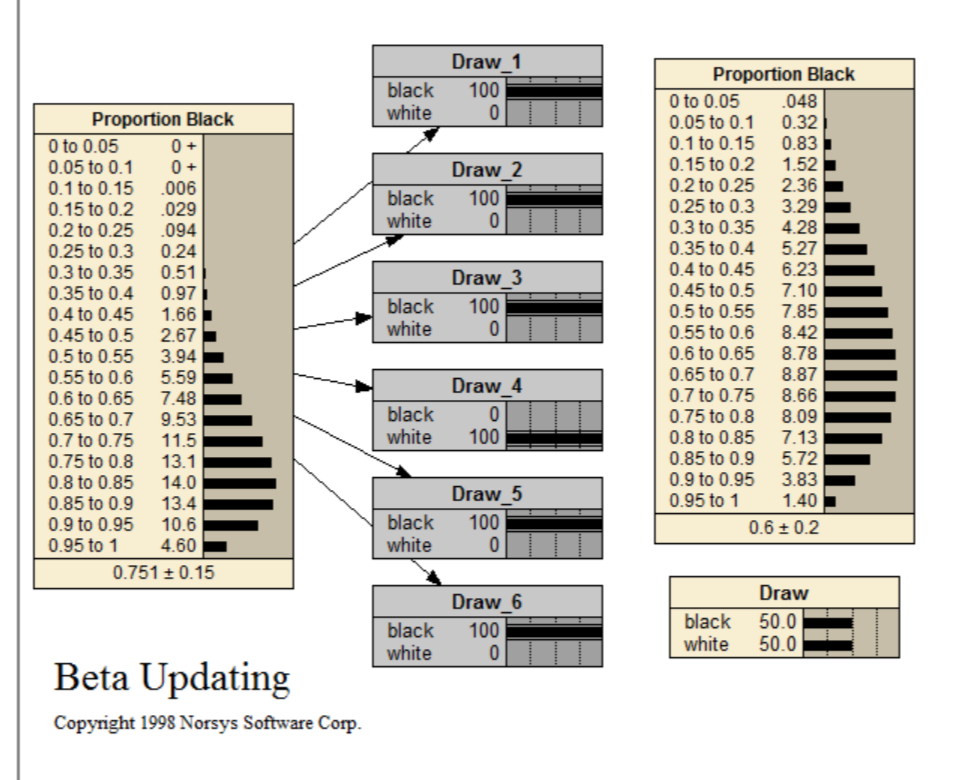
This problem is about how to determine the proportion of white and black balls in a bag. In order to do this, you draw a ball or several balls from the bag and replace them. This can be repeated several times.
This network is also available at <www.norsys.com...> See the tutorial <www.norsys.com...> for more details.
Berkeley Admissions
A demonstration of Simpson's Paradox (also available at <<www.norsys.com...> An explanation of this BN can be found at: <www.norsys.com...>
Socioeconomic Status DBN
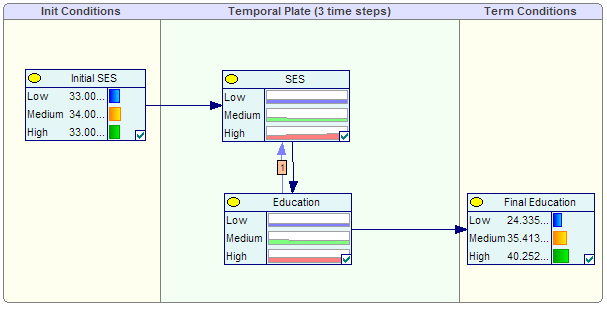
This BN is an example of dynamic Bayesian network which includes feedback loops. The feedback loop represents the commonly accepted feedback relationship between socioeconomic status and education.
 Bayesian Intelligence
Bayesian Intelligence